
|
 |
|
{Page 119}
School of Chemical Engineering and Materials Science, The University of Oklahoma, Norman, Oklahoma
An analytical equation of state for isotropic fluids based on perturbation theory is derived. The PVT properties of the Lennard-Jones (6-12) fluid determined in the Monte Carlo calculations of Verlet and Weis are used to discern the dependence of the equation of state on the temperature-dependent reduced density. The applicability of the equation of state for real fluids is demonstrated using methane PVT data.
| Introduction | Discussion | References | Table of Contents | Home |
In this paper, an analytical equation of state based on perturbation theory is proposed. This equation has a very simple form, involving only a few universal parameters in addition to the Lennard-Jones potential parameters e and s. The equation of state is derived herein, and Monte Carlo PVT data for a Lennard-Jones (6-12) fluid are used to determine the universal parameters. PVT data for methane are then used to demonstrate the applicability of the equation of state for predicting real fluid behavior, and the implications of the results obtained are discussed.
Derivation of the Equation of State
For simple fluids (isotropic fluids) the intermolecular potential f can be expressed in the form
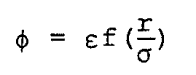 |
Eq. 1 |
where r is the distance between molecule centers, e is the potential strength parameter, and s is the potential distance parameter. The Barker-Henderson (1) and WCA (Weeks, Chandler and Andersen) (2) perturbation theories, which give accurate descriptions of the thermodynamic properties of liquids, are used in the present derivation. The starting point is the following relation for the configurational Helmholtz free energy, A:
 |
Eq. 2 |
where k is the Boltzmann constant, T is the temperature, and Q is the configurational integral
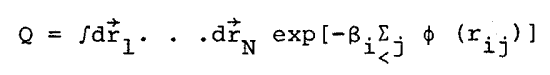 |
Eq. 3 |
where b = 1/kT, ri®is the position vector of the ith molecule, and rij is the distance of separation of molecules i and j. In perturbation theory, real fluid properties are expressed as expansions about the properties of a reference system of hard spheres. The diameter, d, of the hard sphere is determined by making the first order term in the expansion of the configurational Helmholtz free energy equal to zero. Since these theories are well known, only a summary of the important relations will be quoted. The intermolecular potential is separated into two parts, the reference potential, frep, and the perturbation potential, fp,
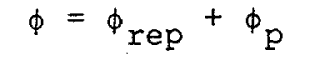 |
Eq. 4 |
where
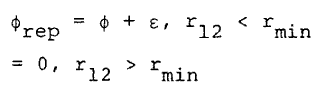 |
Eq. 5 |
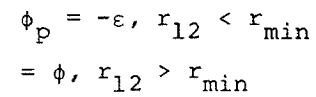 |
Eq. 6 |
where rmin is the separation at which the potential, f, is a minimum. The expansion of the configurational Helmholtz free energy, A, about the reference system free energy, AHS, is, to first order,
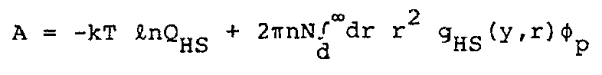 |
Eq. 7 |
where N is the number of molecules of the system, n is the number density, fp is the perturbation part of the potential (discussed below), and y = p nd3/6. The hard sphere diameter, d, is determined by the relation
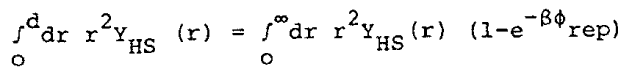 |
Eq. 8 |
{Page 120}
in which gHS (y, r) is the radial distribution function of hard spheres and
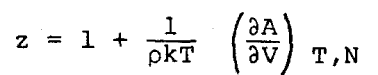 |
Eq. 9 |
The compressibility factor, z, can be obtained from the relation
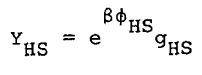 |
Eq. 10 |
so that the following result is obtained from Equation 7,
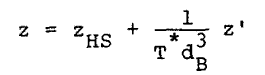 |
Eq. 11 |
where dB = d/s, T* = Tk/e . The term zHS is the hard sphere system compressibility factor, which can be calculated using the Carnahan-Starling equation (3),
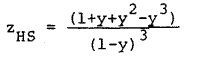 |
Eq. 12 |
The term involving z´ is the perturbation contribution to the compressibility factor, z, where
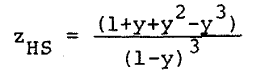 |
Eq. 13 |
The essential step in the derivation of the equation of state presented herein is the observation that the factor z´ is a function of the reduced density, y, only. This can be noted from Equation 13 by virtue of the fact that the radial distribution function for hard spheres, gHS, is a function of r and y only. Thus, the temperature dependence of z´ comes only from the temperature dependence of the hard sphere diameter d, used in calculating the reduced density, y. Therefore, provided that z´ is a slowly varying function of y, a simple equation of state results by treating z´ as an analytical function of y. The advantage of this in equation of state applications is, of course, the fact that the integration of Equation 13 is impractical in most applications, since the dependence of gHS on molecular separation at the density of the real system is required. Thus, the analytical equation of state for isotropic fluids proposed is Equation 11 with the use of Equation 12 for zHS and a simple analytical function of y used for z´.
Lennard-Jones (6-12) Fluid
To test the above idea for an analytical equation of state based on perturbation theory for the case of isotropic fluids, we used the Monte Carlo calculations of Verlet and Weis (4) for the Lennard-Jones (6-12) fluid at T* = 0.75, 1.15, 1.35 and 2.74. The Verlet-Weis formula was used for dB,
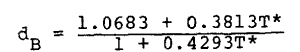 |
Eq. 14 |
The quantity z´LJ for the Lennard-Jones (6-12) fluid obtained using the Monte Carlo compressibility factor values, zMC, was calculated from the relation
| Eq. 15 |
It was noted that a plot of z´LJ versus y yielded a smooth curve with the values of z´LJ for the reduced temperatures of 0.75, 1.15, 1.35 and 2.74 showing very little scatter about the curve. It was determined that z´LJ could be described for the density range of the Verlet-Weis Monte Carlo calculations by a fourth-order polynomial in y,
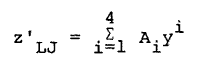 |
Eq. 16 |
This result yields the following relation for the compressibility factor of the Lennard-Jones (6-12) fluid,
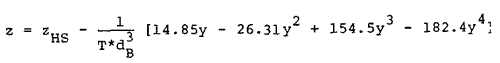 |
Eq. 17 |
The variance, S2, of the calculated compressibility factors was
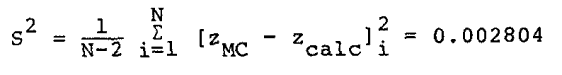 |
Eq. 18 |
where N is the number of points. The average absolute deviation was 1.24%, with absolute deviations ranging from 0.024% to 4.47%. The Verlet-Weis calculated values of zMC have an estimated uncertainty of 2.5%, so the above results are generally within this uncertainty.
Application of Equation of State to Methane PVT Data
The use of the perturbation equation of state in Equation 11 with the polynomial expansion in y for z´, determined from Monte Carlo data, was tested for methane. The values e/k = 148.48 K and s = 3.695 Å were determined by regression on PVT data in the reduced temperature range 2.46<T*<8.70 and reduced density range 0.03<r*<0.08, where T* = kT/e and r* = r N s 3, where N is Avogadro's number. The regression yielded a standard de-
{Page 121}
viation of 0.0199 and an average absolute deviation of 1.26% for predicted densities when compared with the data of van Itterbeek (6), Vennix (7), and Douslin (8). Since methane is not exactly a Lennard-Jones (6-12) fluid, the parameters e and s are really the average potential strength and average potential range for the type and range of data used in their determination. Thus, the values of e /k and s determined in these calculations differ from the values reported by Hirschfelder, Curtiss and Bird (5) obtained by fitting the second virial coefficient (e /k = 148.2 K, s = 3.817 Å). Calculated densities are compared with experimental data for methane in Table 1. It can be noted in Table 1 that liquid densities predicted by the equation of state are generally within 0.3% of the experimental values, while deviations in the vapor phase are generally about 2%. The larger vapor phase deviations are due mainly to the inadequacy of the second virial coefficient in Equation 17. Even with the noted vapor phase deviations, the results in Table 1 are sufficiently good to justify use of the new equation of state in many practical applications.
| Introduction | Discussion | References | Table of Contents | Home |
The study presented herein shows that it is possible to develop analytical equations of state based on perturbation theory. The equation of state formula derived in this study has been used to describe the PVT behavior of methane with reasonable accuracy. It is expected that the equation of state can be improved by modification of the density and temperature dependence of the equation. The density dependence can be modified simply by using a higher order expansion in the reduced density for the perturbation part of the compressibility factor. The temperature dependence can be modified by allowing the constants in the Verlet-Weis formula for dB to be parameters to be determined by regression, and/or by modification of the temperature dependence of the equation of state as implied by higher order perturbation theory (1, 2). These modifications will be investigated in future work.
This research was sponsored by the American Gas Association.
| Introduction | Discussion | References | Table of Contents | Home |
1. J. A. BARKER and D. HENDERSON, J. Chem. Phys. 47: 2861-4716 (1967).
2. J. D. WEEKS, D. CHANDLER, and H. C. ANDERSEN, JR., Phys. Rev. Lett. 25: 149 (1970); J. Chem. Phys. 54: 5237 (1971).
3. N. F. CARNAHAN and K. E. STARLING, J. Chem. Phys. 51: 635 (1969).
4. L. VERLET and J. J. WEIS, Phys. Rev. A5: 939 (1972).
5. J. O. HIRSCHFELDER, C. F. CURTISS, and R. B. BIRD, Molecular Theory of Gases and Liquids, John Wiley, New York, 1954.
6. A. VAN ITTERBEEK, O. VERBEKE, and K. STAES, Physica 29: 742 (1963).
7. A. J. VENNIX, Low Temperature Volumetric Properties and the Development of an Equation of State for Methane, Ph.D. dissertation, Rice University, 1966.
8. D. R. DOUSLIN, R. H. HARRISON, R. T. MOORE, and J. P. McCULLOUGH, J. Chem. Engr. Data 9: 358 (1964).
| Introduction | Discussion | References | Table of Contents | Home |