
|
 |
|
{Page 138}
Fiber Industries, Inc., Archdale Drive, Charlotte, North Carolina, and
School of Chemical Engineering and Materials Science, University of Oklahoma, Norman, Oklahoma
Glucose-6-phosphate dehydrogenase has been insolubilized by covalent bonding to glass beads. A batch recirculation reactor relatively free from concentration gradients and diffusion limitations has been used to determine the rates of reaction. The pH and temperature of local maximum enzymatic activity have been determined. While these operating parameters do not represent the true optima, they have aided in routinely regenerating NADPH in small quantities in this laboratory.
| Introduction | Materials | Results and Discussion | References | Table of Contents | Home |
Recent work in this laboratory has involved the production of N-oxides and other metabolites of various clinically useful drugs for characterization and for toxicological studies. This has led to the development of reactors charged with insolubilized enzymes capable of in vitro production of drug metabolites in relatively large (milligram) quantities. The reactions normally have a requirement for a cofactor or a cosubstrate (hereinafter referred to as cofactor). For example, in the following N-oxidation reaction involving a mixed- function flavoprotein oxidase (MFMF), there is a requirement of NADPH
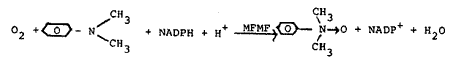
In view of the fact that NADPH costs $250/gram, this raises an obvious economic problem. The regeneration of cofactor has been proposed to help alleviate the costs of these reactions. The enzymes glucose-6-phosphate dehydrogenase and lactate dehydrogenase can be immobilized on solid matrices and used to regenerate NADPH from NADP+. A tenfold regeneration in this case yields a savings of $225/g.
Significant progress has been made in the recent past in the areas collectively referred to as enzyme technology (3, 6, 11). With insolubilized enzymes, one may recover the solid support to obtain the enzyme for reuse, thus overcoming one of the major economic drawbacks to the extensive use of these enzymes in the production of various compounds. In addition, the insolubilized forms of many enzymes appear to be more stable to environmental conditions than do the free enzymes in solution (10). While this is not always the case, the proper type of immobilization may render an inherently less stable intercellular enzyme sufficiently stable for use in the variety of noncellular reactors.
While much progress has been made in the recent past in the area of enzyme technology, direct application of the reactions involving cofactors has lagged somewhat behind, particularly because of the high cost of most of these cofactors. Further considerations on the use of cofactor-requiring enzymes in enzyme engineering are presented in an excellent review by Baricos, Chambers and Cohen (1).
Glucose-6-phosphate dehydrogenase (G6PD) was first described by Warburg and his co-workers (7, 8), who demonstrated NADP+ to be a specific coenzyme. The enzyme functions very well in glycylglycine buffer at pH 7.5. Mg2+ stimulates the reaction. Phosphate buffer has been known to inhibit the enzyme (2). The reaction is monitored spectrophotometrically at 340 nm by the formation of NADPH.
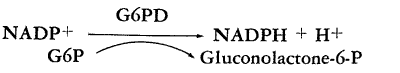
D![]() for the above reaction has been calculated (9) to be +5400 cal/mole at 25 C.
for the above reaction has been calculated (9) to be +5400 cal/mole at 25 C.
{Page 139}
| Introduction | Materials | Results and Discussion | References | Table of Contents | Home |
Glucose-6-phosphate dehydrogenase was obtained from Sigma Chemical Company. NADP+ was obtained from P-L Biochemical Incorporated. Glycylglycine was purchased from Aldrich Chemical Company, and glutaraldehyde from Mathieson, Coleman and Bell. Glass beads were obtained
{Page 140}
from Pierce Chemical Company, Rockford, Illinois.
Enzyme was bound to zirconia-clad porous glass beads (1350 Angstrom pore diameter) according to directions supplied by Pierce Chemical Company (5). Glutaraldehyde (40 ml, 2.5 wt %) was added to 4 g glass beads. The mixture was kept in a vacuum (water aspirator) for 30 min to remove air bubbles. The vacuum was then released and the reaction continued at ambient temperature and pressure for another 40 min. The glutaraldehyde solution was carefully decanted and the beads were washed at least 10 times with 30-ml portions of water. Then G6PD solution (4 ml, 20 units per ml) was added to the activated beads on ice slurry and reaction was allowed to continue in vacuum for 30 min after which the beads were placed in a refrigerator overnight at ambient pressure. The catalyst thus prepared was washed five times with 10-ml portions of glycylglycine buffer and stored in the buffer solution at 4 C.
The flow reactors were charged with insolubilized enzyme; the reaction medium contained 1.5 × 10–3 M NADP+, 1.5 × 10–3 M G6P, and 0.04 M glycylglycine buffer of pH 7.6 in a typical volume of 3.5 ml.
A spectrophotometer operating at 340 nm was used to determine the optical density change of the medium as a function of time.
In the fluidized-bed reactor (Figure 1), the reaction medium is withdrawn from a reservoir, pumped into a fluidized catalyst bed and recycled into the same reservoir as needed. The reactor is made of glass and
{Page 141}
temperature is controlled by circulating water through the surrounding jacket.
For the batch-recirculation mode (Figure 2), the fixed-bed reactor is operated with high fluid velocities such that the concentration gradients across the bed are relatively low.
| Introduction | Materials | Results and Discussion | References | Table of Contents | Home |
Figure 3 illustrates yield as a function of pH at 23 C. To calculate the activity as a function of pH, the average slope of each curve in Figure 3 was plotted against its respective pH. Figure 4 results from these calculations. The maximum enzymatic activity exists at pH 7.5 ± 0.2. This value corresponds very closely with the value for the enzyme in solution. In order to maximize production per unit enzyme as a function of pH, the plot of catalyst half-life with respect to pH was obtained and is shown in Figure 5. From Figures 4 and 5 it is possible to calculate maximum product yield as a function of pH. Figure 6 results from these calculations. The ordinate was calculated by assuming a first-order decomposition of catalyst with respect to time and integrating over time from zero to infinity. It is reasonable that the rate gains obtained by operating at pH 7.5 ± 0.2 could be upset in the lower pH region by the lower rate of catalyst deactivation in that range.
Another variable affecting the catalyst activity is temperature. Figure 7 illustrates yield as a function of time at pH 7.5. The activity as a function of temperature is calculated the same way Figure 4 was derived and the result is illustrated in Figure 8. The
{Page 142}
maximum enzymatic activity exists at 37 C, which also corresponds closely with that of the enzyme in solution. As in the case with pH, a plot of catalyst half-life with respect to temperature is required to determine the maximum production per unit enzyme as a function of temperature. This plot is shown in Figure 9. From Figures 8 and 9, the maximum possible product yield as a function of temperature is obtained. The optimum range at 30 C is shown in Figure 10.
Several possible limitations exist in advancing the use of insolubilized enzyme reactors. These limitations include diffusional restrictions both in the transfer of the substrate molecule to the external surface of the catalyst and in its transfer into the interior of the catalyst where much of the reaction proceeds. The diffusional limitation of access to the external surface was determined using an external diffusion test which involves varying the flow rate and determining the rate of reaction. The effect of internal diffusion may be determined by using an enzyme loading test. It is demonstrated elsewhere that neither of these
{Page 143}
diffusional limitations exists in this case (4). The Michaelis-Menten constants were determined from the Lineweaver-Burke plot shown in Figure 10. Vmax and KM were calculated to be 2.3 × 10–7 mole/g dry beads/ min and 3.5 × 10–5 mole/l, respectively.
We are unable at this time to describe quantitatively and reproducibly the deactivation characteristics of immobilized G6PD. Such a description would provide the feedback necessary for perhaps modifying insolubilization techniques and decreasing activity losses and enable us to provide information for a more adequate reactor design. Further, global optima for these operating parameters such as temperature and pH have not been calculated. However, local maximizations have aided in routinely producing NADPH inexpensively and in sufficient quantities in this laboratory.
| Introduction | Materials | Results and Discussion | References | Table of Contents | Home |
1. W. BARICOS, R. CHAMBERS, and W. COHEN, Enzyme Technol. Dig. 4: 39 (1975).
2. L. GLOSER and D. H. BROWN, J. Biol. Chem. 216: 77 (1955).
3. KLAUS MOSBACH, Sci. Am. 224 (3): 26 (March 1971).
4. V. O. ORELAJA, Master's Thesis, University of Oklahoma, Norman, Oklahoma, 1976.
5. Pierce Previews, Published by Pierce Company, Rockford, Illinois, U.S.A., April, 1973.
6. G. R. STARK, (ed.), Biochemical Aspects of Reactions on Solid Supports, Academic Press, New York, N.Y., 1971.
7. O. WARBURG and W. CHRISTIAN, Biochem. Z. 242: 206 (1931).
8. O. WARBURG and W. CHRISTIAN, Biochem. Z. 287: 440 (1936).
9. O. WARBURG, W. CHRISTIAN, and A. BRIESE, Biochem Z. 282: 157 (1935).
10. L. B. WINGARD, JR., Enzyme Engineering, John Wiley and Sons, New York, N.Y., 1972.
11. O. R. ZARBORSKY, Immobilized Enzymes, The Chemical Rubber Company, Cleveland, 1973.
| Introduction | Materials | Results and Discussion | References | Table of Contents | Home |